Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 스프링 mvc2 - 타임리프
- 스프링 입문(무료)
- 스프링 mvc1 - 서블릿
- 자바의 정석 기초편 ch2
- 자바의 정석 기초편 ch1
- 코드로 시작하는 자바 첫걸음
- 스프링 mvc1 - 스프링 mvc
- 자바의 정석 기초편 ch3
- jpa 활용2 - api 개발 고급
- 스프링 mvc2 - 검증
- 2024 정보처리기사 시나공 필기
- 자바의 정석 기초편 ch13
- 스프링 mvc2 - 로그인 처리
- jpa - 객체지향 쿼리 언어
- 게시글 목록 api
- 타임리프 - 기본기능
- 자바의 정석 기초편 ch12
- 자바의 정석 기초편 ch11
- 자바의 정석 기초편 ch6
- 자바의 정석 기초편 ch4
- 자바의 정석 기초편 ch5
- 자바의 정석 기초편 ch7
- 스프링 db1 - 스프링과 문제 해결
- 2024 정보처리기사 수제비 실기
- 자바의 정석 기초편 ch8
- @Aspect
- 스프링 고급 - 스프링 aop
- 스프링 db2 - 데이터 접근 기술
- 자바의 정석 기초편 ch9
- 자바의 정석 기초편 ch14
Archives
- Today
- Total
나구리의 개발공부기록
1장 - 데이터 입・출력 구현 | 섹션1. 자료구조, 섹션2. 트리(Tree) 본문
2024정보처리기사 준비 정리(필기 - 시나공, 실기 - 수제비)/필기 2강 - 소프트웨어 개발
1장 - 데이터 입・출력 구현 | 섹션1. 자료구조, 섹션2. 트리(Tree)
소소한나구리 2024. 4. 18. 21:062024년도 시나공 필기 책 내용 정리
섹션1. 자료구조
1. 자료구조
- 효율적인 프로그램을 작성할 때 가장 우선적인 고려사항은 저장 공간의 효율성과 실행시간의 신속성임
- 자료 구조는 프로그램에서 사용하기 위한 자료를 기억장치의 공간 내에 저장하는 방법과 저장된 그룹 내에서 존재하는 자료간의 관계, 처리 방법 등을 연구 분석하는 것을 말함
선형 구조(Linear Structure)
- 배열(Array)
- 선형 리스트(Linear List)
- 연속 리스트(Contiguous List)
- 연결 리스트(Linked List)
- 스택(Stack)
- 큐(Queue)
- 데크(Deque)
비 선형 구조
- 트리(Tree)
- 그래프(Graph)
2. 배열(Array)
- 동일한 자료형의 데이터들이 같은 크기로 나열되어 순서를 갖고 있는 집합
- 정적인 자료 구조로 기억장소의 추가가 어렵고, 데이터 삭제 시 데이터가 저장되어 있던 기억장소는 빈 공간으로 남아있어 메모리의 낭비가 발생함
- 첨자를 이용하여 데이터에 접근함
- 반복적인 데이터 처리에 적합한 구조
- 데이터마다 동일한 이름의 변수를 사용하여 처리가 간편함
- 사용한 첨자의 개수에 따라 n차원 배열이라고 부름
3. 선형 리스트(Linear List)
- 일정한 순서에 의해 나열된 자료 구조
- 배열을 이용하는 연속 리스트(Contiguous List)와 포인터를 이용하는 연결 리스트(Linked List)로 구분됨
연속 리스트(Contiguous List)
- 배열과 같이 연속되는 기억장소에 저장되는 자료 구조
- 기억장소를 연속적으로 배정받기 때문에 기억장소 이용 효율은 밀도가 1로서 가장 좋음
- 중간에 데이터를 삽입하기 위해서는 연속된 빈 공간이 있어야 하며, 삽입 및 삭제 시 자료의 이동이 필요함
연결 리스트(Linked List)
- 자료들을 반드시 연속적으로 배열시키지는 않고 임의의 기억공간에 기억시키되 자료 항목의 순서에 따라 노드의 포인터 부분을 이용하여 서로 연결시킨 자료 구조
- 노드의 삽입, 삭제 작업이 용이함
- 기억 공간이 연속적으로 놓여 있지 않아도 저장할 수 있음
- 연결을 위한 링크(포인터) 부분이 필요하기 때문에 순차 리스트에 비해 기억 공간의 이용 효율이 좋지 않음
- 연결을 위한 포인터를 찾는 시간이 필요하기 때문에 접근 속도가 느림
- 중간 노드 연결이 끊어지면 그 다음 노드를 찾기 힘듦
4. 스택 (Stack)
- 리스트의 한쪽 끝으로만 자료의 삽입, 삭제 작업이 이루어지는 자료 구조
- 가장 나중에 삽입된 자료가 가장 먼제 삭제되는 후입선출(LIFO: Last In First Out) 방식으로 자료를 처리함
- Stack의 응용분야 : 함수의 호출 순서 제어, 인터럽트 처리, 수식 계산 및 수식 표기법, 컴파일러를 이용한 언어 번역, 부 프로그램 호출 시 복귀 주소 저장, 서브 루틴 호출 및 복귀 주소 저장
- 스택의 모든 기억 공간이 꽉 채워져 있는 상태에서 데이터가 삽입되면 오버플로가 발생되며 더 이상 삭제할 데이터가 없는 상태에서 데이터를 삭제하면 언더플로가 발생함
- TOP : 스택으로 할당된 기억 공간에 가장 마지막으로 삽입된 자료가 기억된 위치를 가리키는 요소
- Bottom : 스택의 가장 밑바닥
- Push : 자료의 삽입
- M : 스택의 크기
- TOP : 스택 포인터
- X : 스택의 이름
- Overflow : 스택으로 할당받은 메모리 부분의 마지막 주소가 M번지라고 할 때, Top Pointer의 값이 M번지보다 커지면 스택의 모든 기억장소가 꽉 채워져 있는 상태이므로 더 이상 자료를 삽입할 수 없어 Overflow를 발생 시킴
- Pop Up : 자료의 삭제
- Stack에 기억되어 있는 자료를 삭제시킬 때는 제일 먼저 삭제할 자료가 있는지 없는지부터 확인해야함
- Underflow : Top Pointer가 주소 0을 가지고 있다면 스택에는 삭제할 자료가 없으므로 Underflow를 발생시킴
순서가 A, B, C, D로 정해진 입력 자료를 스택에 입력하였다가 B, C, D, A 순서로 출력되는 과정을 나열
- PUSH A -> PUSH B -> POP B -> PUSH C -> POP C -> PUSH D -> POP D -> POP A
5. 큐(Queue)
- 리스트의 한쪽에서는 삽입 작업이 이루어지고 다른 한쪽에서는 삭제 작업이 이루어지도록 구성한 자료구조
- 가장 먼저 삽입된 자료가 가장 먼저 삭제되는 선입선출(FIFO: First In First Out) 방식으로 처리됨
- 시작과 끝을 표시하는 두 개의 포인터가 있음
- 프런트(F, Front) 포인터 : 가장 먼저 삽입된 자료의 기억 공간을 가리키는 포인터로 삭제 작업을 할 때 사용됨
- 리어(R, Rear) 포인터 : 가장 마지막에 삽입된 자료가 위치한 기억 공간을 가리키는 포인터로 삽입 작업을 할 때 사용됨
6. 데크(Deque)
- 삽입과 삭제가 리스트의 양쪽 끝에서 모두 발생할 수 있는 자료 구조
- Double Ended Queue의 약자
- Stack 과 Queue의 장점만 따서 구성한 것
- 입력이 한쪽에서만 발생하고 출력은 양쪽에서만 일어날 수 있는 입력 제한과 입력은 양쪽에서 일어나고 출력은 한 곳에서만 이루어지는 출력제한이 있음
- 입력 제한 데크 : Scroll
- 출력 제한 데크 : Shelf
7. 그래프(Graph)
- 그래프(G)는 정점 V(Vertex)와 간선 E(Edge)의 두 집합으로 이루어짐
- 간선의 방향성 유무에 따라 방향 그래프와 무방향 그래프로 구분됨
- 통신망(Network), 교통망, 이항관계, 연립방정식, 유기화학 구조식, 무향선분 해법 등에 응용됨
- 트리(Tree)는 사이클이 없는 그래프(Graph)임
방향/무방향 그래프의 최대 간선 수
- n개의 정점으로 구성된 무방향 그래프에서 최대 간선수는 n(n-1)/2
- n개의 정점으로 구성된 방향 그래픙서 최대 간선수는 n(n-1)
섹션2. 트리(Tree)
1. 트리의 개요
- 정점(Node, 노드)과 선분(Branch, 가지)을 이용하여 사이클을 이루지 않도록 구성한 그래프(Graph)의 특수한 형태
- 하나의 기억 공간을 노드(Node)라고 하며 노드와 노드를 연결하는 선을 링크(Link)라고 함
- 가족의 계보(족보), 조직도 등을 표현하기에 적합함
트리 관련 용어
- 최상위 노드부터 level1 ... -> 마지막 레벨 -> Depth 구조
- 노드(Node) : 트리의 기본 요소로서 자료 항목과 다른 항목에 대한 가지(Branch)를 합친 것
- 근 노드(Root Node) : 트리의 맨 위에 있는 노드
- 디그리(Degree, 차수) : 각 노드에서 뻗어 나온 가지의 수
- 단말 노드(Terminal Node) = 잎 노드(Leaf Node) : 자식이 하나도 없는 노드, 즉 디그리가 0인 노드
- 자식 노드(Son Node) : 어떤 노드에 연결된 다음 레벨의 노드들
- 부모 노드(Parent Node) : 어떤 노드에 연결된 이전 레벨의 노드들
- 형제 노드(Brother Node, Sibiling) : 동일한 부모를 갖는 노드들
- 트리의 디그리 : 노드들의 디그리 중에서 가장 많은 수
2. 트리의 운행법
- 트리를 구성하는 각 노드들을 찾아가는 방법을 운행법(Traversal)이라 함
- 산술식의 표기법과 연관성을 갖으며 세가지의 운행 방법이 있음
- Preorder 운행 : Root -> Left -> Right 순으로 운행
- Inorder 운행 : Left -> Root -> Right 순으로 은행
- Postorder 운행 : Left -> Right -> Root 순으로 운행
아래의 트리를 Preorder, Inorder, Postorder방법으로 운행했을 때 각 노드를 방문한 순서를 작성

- Preorderd : A -> B -> D -> H -> I -> E -> C -> F -> G
- Inorder : H -> D -> I -> B -> E -> A -> F -> C -> G
- Postorder : H -> I -> D -> E -> B -> F -> G -> C -> A
3. 수식의 표기법
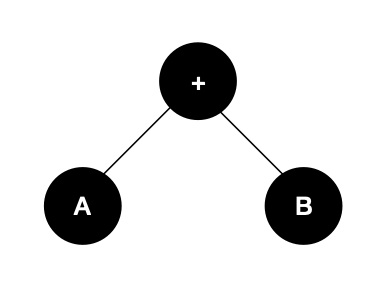
- 산술식을 계산하기 위해 기억공간에 기억시키는 방법으로 이진 트리를 많이 사용함
- 이진 트리로 만들어진 수식을 인오더, 프리오더, 포스트오더로 운행하면 각각 중위(Infix), 전위(Prefix), 후위(Postfix) 표기법이 됨
- 전위 표기법(PreFix) : 연산자 -> Left -> Right / +AB
- 중위 표기법(InFix) : Left -> 연산자 -> Right / A+B
- 후위 표기법(PostFix) : Left -> Right -> 연산자 / AB+
Infix 표기를 Postfix나 Prefix로 바꾸기
- Postfix나 Prefix는 스택을 이용하여 처리하므로 Infix는 Postfix나 Prefix로 바꾸어 처리함
다음의 Infix로 표기된 수식을 Prefix와 Postfix로 변환, X = A / B * (C + D) + E
- 연산 우선순위에 따라 괄호로 묶고, 연산자를 해당 괄호의 앞(Prefix로 변환), 뒤(Postfix)로 변환 옮기고 필요 없는 괄호를 제거
- (X = (((A / B) * (C + D) + E ))
- Prefix로 변환 : = X + * / A B + C D E
- Postfix로 변환 : X A B / C D + * E + =
Postfix나 Prefix로 표기된 수식을 Infix로 바꾸기
- Posffix는 Infix표기법에서 연산자를 해당 피연산자 두 개의 뒤로 이동한 것이므로 연산자를 다시 피연산자의 가운데로 옮기면 됨
- Prefixs는 반대로 연산자를 해당 피연산자 두개의 앞으로 이동한 것, 마찬가지로 다시 피연산자의 가운데로 옮기면 됨
다음의 Postfix 수식을 Infix로 변환, A B C - / D E F + * +
- 인접한 피연산자 두 개와 오른쪽의 연산자를 괄호로 묶고, 연산자를 해당 피연산자의 가운데로 이동 시킨 후 필요없는 괄호를 제거
- ((A (B C - ) /) (D (E F +) *) +)
- Infix로 변환 : A / (B - C) + D * (E + F)
다음의 Prefix 수식을 Infix로 변환, + / A - B C * D + E F
- 인접한 피연산자 두개와 왼쪽의 연산자를 괄호로 묶고, 연산자를 해당 피연산자의 가운데로 이동 시킨 후 필요없는 괄호를 제거
- (+ (/ A (- B C)) (* D (+ E F))
- Infix로 변환 : A / (B - C) + D * (E + F)
'2024정보처리기사 준비 정리(필기 - 시나공, 실기 - 수제비) > 필기 2강 - 소프트웨어 개발' 카테고리의 다른 글
| 2장 - 통합 구현 핵심 요약 (0) | 2024.04.27 |
|---|---|
| 2장 - 통합 구현 | 섹션7. 단위 모듈 구현, 섹션8. 단위 모듈 테스트, 섹션9. 개발 지원 도구 (0) | 2024.04.25 |
| 1장 - 데이터 입・출력 구현 핵심 요약 (0) | 2024.04.24 |
| 1장 - 데이터 입・출력 구현 | 섹션5. 데이터베이스 개요, 섹션6. 절차형SQL (0) | 2024.04.23 |
| 1장 - 데이터 입・출력 구현 | 섹션3. 정렬(Sort), 섹션4. 검색 - 이분 검색 / 해싱 (0) | 2024.04.23 |

