Notice
Recent Posts
Recent Comments
Link
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
Tags
- 자바의 정석 기초편 ch1
- 스프링 입문(무료)
- 자바의 정석 기초편 ch11
- 자바로 계산기 만들기
- 자바 고급2편 - io
- 자바의 정석 기초편 ch4
- @Aspect
- 데이터 접근 기술
- 자바로 키오스크 만들기
- 2024 정보처리기사 시나공 필기
- 람다
- 자바의 정석 기초편 ch12
- 자바 기초
- 스프링 mvc2 - 검증
- 자바의 정석 기초편 ch7
- 자바의 정석 기초편 ch13
- 자바 중급1편 - 날짜와 시간
- 스프링 mvc2 - 로그인 처리
- 자바의 정석 기초편 ch2
- 스프링 고급 - 스프링 aop
- 자바의 정석 기초편 ch5
- 자바 고급2편 - 네트워크 프로그램
- 스프링 mvc1 - 스프링 mvc
- 2024 정보처리기사 수제비 실기
- 스프링 트랜잭션
- 자바의 정석 기초편 ch9
- 스프링 mvc2 - 타임리프
- 자바의 정석 기초편 ch14
- 자바 중급2편 - 컬렉션 프레임워크
- 자바의 정석 기초편 ch6
Archives
- Today
- Total
개발공부기록
컬렉션 프레임워크 - Set, 자바가 제공하는 Set(HashSet, LinkedHashSet, TreeSet, 예제, 최적화) 본문
자바 로드맵 강의/중급 2 - 컬렉션 프레임워크
컬렉션 프레임워크 - Set, 자바가 제공하는 Set(HashSet, LinkedHashSet, TreeSet, 예제, 최적화)
소소한나구리 2025. 2. 6. 17:56728x90
출처 : 인프런 - 김영한의 실전 자바 - 중급2편 (유료) / 김영한님
유료 강의이므로 정리에 초점을 두고 코드는 일부만 인용
1. 자바가 제공하는 Set
1) HashSet, LinkedHashSet

(1) 컬렉션 프레임워크 - Set 인터페이스
- java.util 패키지의 컬렉션 프레임워크에 속하는 인터페이스 중 하나
- Set 인터페이스는 중복을 허용하지 않는 유일한 요소의 집합을 나타내어 어떤 요소도 같은 Set 내에 두 번 이상 나타날 수 없음
- Set은 수학적 집합 개념을 구현한 것으로 순서를 보장하지 않고 특정 요소가 집합에 있는지 여부를 확인하는데 최적화 되어있음
- 구현체로는 HashSet, LinkedHashSet, TreeSet 등이 있으며 각 클래스는 각각의 특성을 가지고 있음
(2) Set 인터페이스의 주요 메서드
- List와 비슷하지만 인덱스로 조회하는 메서드가 없음
| 메서드 | 설명 |
| add(E e) | 지정된 요소를 세트에 추가하고 이미 존재하면 추가하지 않음 |
| addAll(Collection<? extends E> c) | 지정된 컬렉션의 모든 요소를 세트에 추가 |
| contains(Object o) | 세트가 지정된 요소를 포함하고 있는지 여부를 반환 |
| containsAll(Collection<?> c) | 세트가 지정된 컬렉션의 모든 요소를 포함하고 있는지 여부를 반환 |
| remove(Object o) | 지정된 요소를 세트에서 제거 |
| removeAll(Collection<?> c) | 지정된 컬렉션에 포함된 요소를 세트에서 모두 제거 |
| clear() | 세트에서 모든 요소를 제거 |
| retainAll(Collection<?> c) | 지정된 컬렉션에 포함된 요소만을 유지하고 나머지 요소는 세트에서 제거 |
| size() | 세트의 요소 수를 반환 |
| isEmpty() | 세트가 비어있는지 여부를 반환 |
| iterator() | 세트의 요소에 대한 반복자를 반환 |
| toArray() | 세트의 모든 요소를 배열로 반환 |
| toArray(T[] a) | 세트의 모든 요소를 지정된 배열로 반환 |
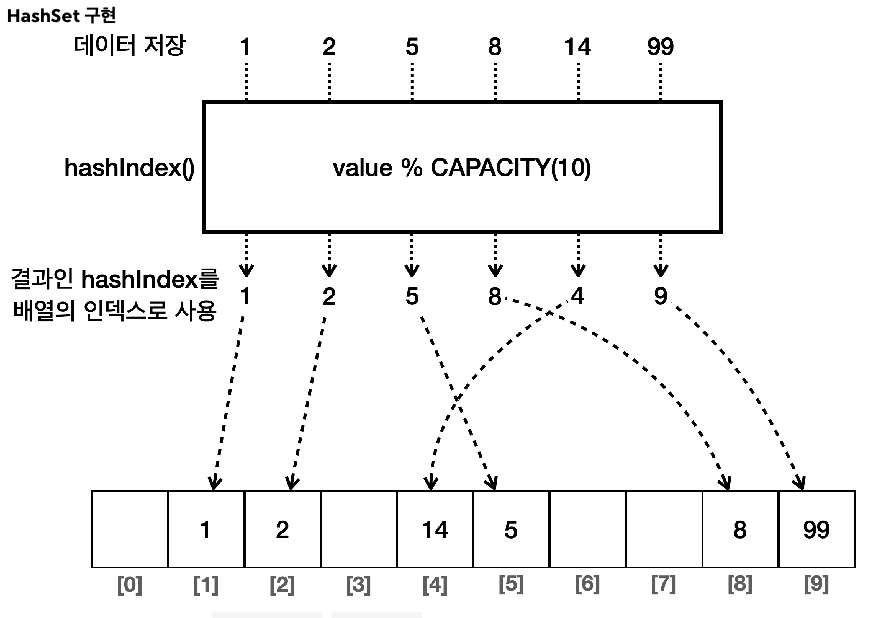
(3) HashSet
- 구현: 해시 자료 구조를 사용해서 요소를 저장
- 순서: 요소들은 특정한 순서 없이 저장되므로 요소를 추가한 순서를 보장하지 않음
- 시간 복잡도: HashSet의 주요연산(추가, 삭제, 검색)은 평균적으로 O(1)의 시간 복잡도를 가짐
- 용도: 데이터의 유일성만 중요하고 순서가 중요하지 않은 경우에 적합함
(4) LinkedHashSet
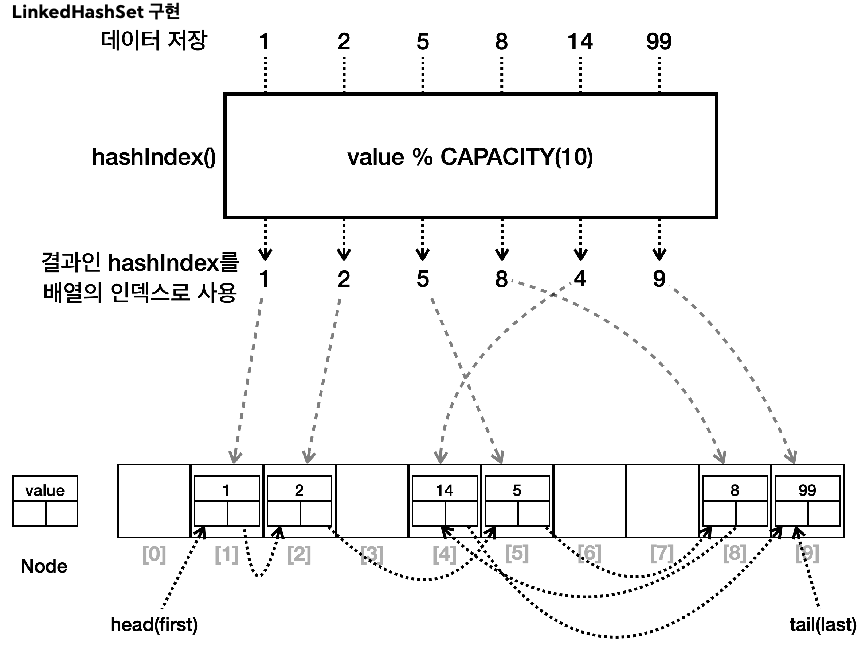
- 구현
- HashSet에 연결 리스트를 추가해서 요소들의 순서를 유지하며 HashSet에 LinkedList를 합친 것으로 이해하면 됨
- head(first)부터 순서대로 링크를 따라가면 입력 순서대로 데이터를 순회할 수 있으며 양방향으로 연결됨
- 순서: 요소들이 추가된 순서대로 유지되므로 순서대로 조회 시 요소들이 추가된 순서대로 반환됨
- 시간 복잡도: 주요 연산에 대해 평균 O(1) 시간 복잡도를 가짐
- 용도: 데이터의 유일성과 함께 삽입 순서를 유지해야 할 때 적합함
- 참고
- 연결 링크를 유지해야 하기 때문에 HashSet 보다는 조금 더 무거움
- LinkedHashSet은 순서를 보장하지만 Set은 일반적으로 순서를 보장하지 않는 자료 구조이기 때문에 Set 인터페이스를 사용하면 기본적으로는 순서 보장이 안 된다고 가정하고 사용해야하며, Set을 사용하지만 순서 보장이 필요할 때 LinkedHashSet을 사용하면 됨
2) TreeSet
(1) TreeSet
- 구현: TreeSet은 이진 탐색 트리를 개선한 레드-블랙 트리를 내부에서 사용함
- 순서: 요소들은 정렬된 순서로 저장되는데, 순서의 기준은 비교자(Comparator)로 변경할 수 있음
- 시간 복잡도: 주요 연산들은 O(log n)의 시간 복잡도를 가지므로 HashSet보다는 느림
- 용도
- 데이터들을 정렬된 순서로 유지하면서 집합의 특성을 유지해야 할 때 사용함
- 범위 검색이나 정렬된 데이터가 필요한 경우에 유용하며 입력된 순서가 아니라 데이터 값의 순서로 정렬됨
- ex) 3, 1, 2 순서대로 데이터를 입력 -> 1, 2, 3 순서로 출력
(2) 트리 구조
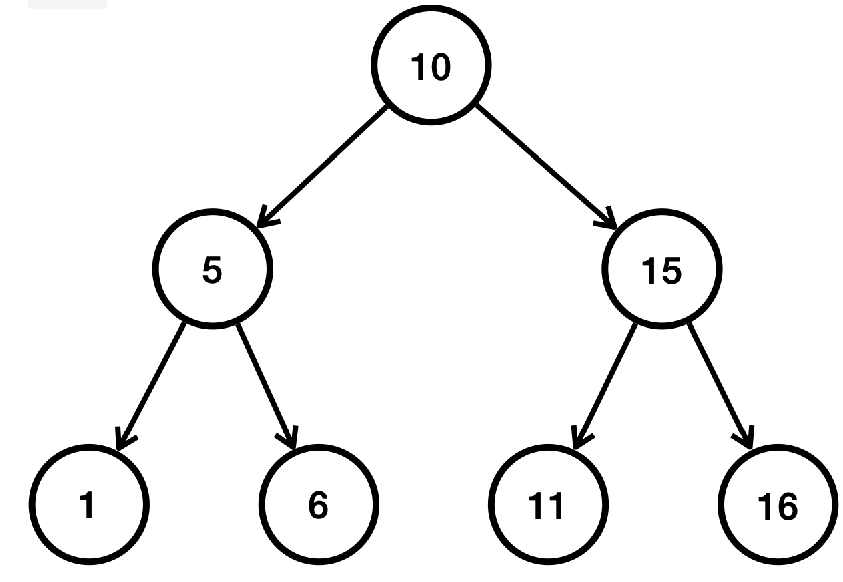
- 트리는 부모 노드와 자식 노드로 구성됨
- 가장 높은 조상을 루트(root)라고 함
- 자식이 2개까지 올 수 있는 트리를 이진 트리라고 함
- 여기에 노드의 왼쪽 자손은 더 작은 값을 가지고 오른쪽 자손은 더 큰 값을 가지는 것을 이진 탐색 트리라고 함
- TreeSet은 이진 탐색 트리를 개선한 레드-블랙 트리를 사용하는데 기본 개념은 이진 탐색 트리와 비슷함
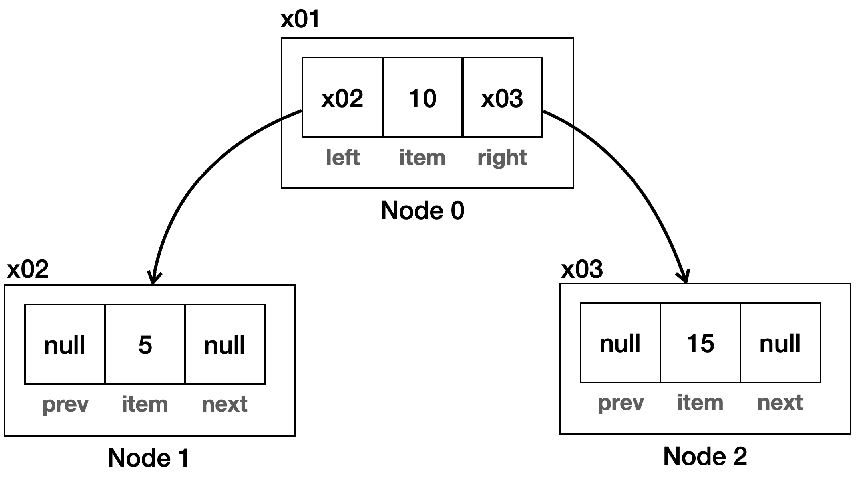
(3) 트리 구조의 구현
- 트리의 구조는 왼쪽, 오른쪽 노드를 알고 있으면 되는데 앞서 다룬 연결 리스트의 구현과 매우 흡사한 것을 알 수 있음
(4) 이진 탐색 트리 - 입력 예시
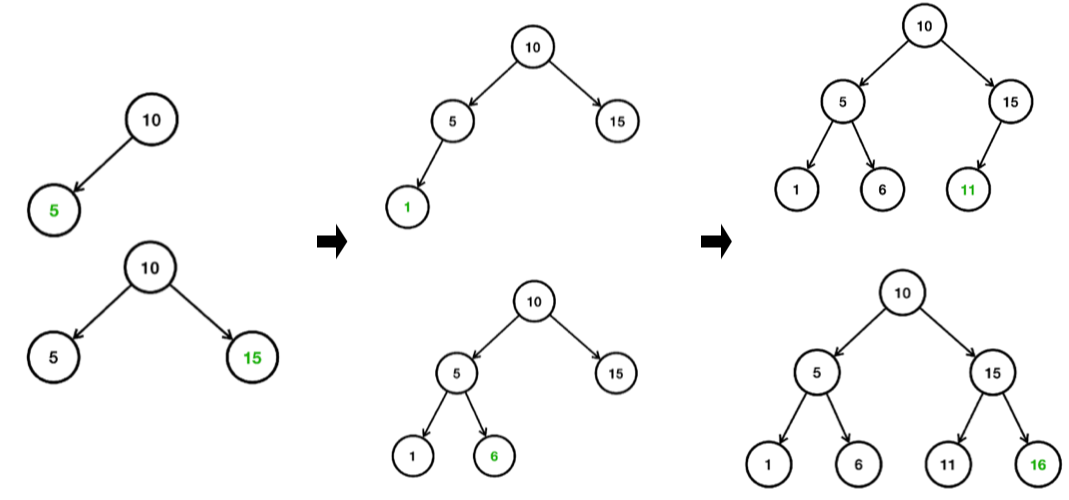
- 이진 탐색 트리의 핵심은 데이터를 입력하는 시점에 정렬해서 보관한다는 점임
- 10, 5, 15, 1, 6, 11, 16 순서대로 입력한다고 가정하면 10을 입력 후 5를 입력하면 5는 10보다 작으므로 왼쪽에 저장되고 그다음 저장되는 15는 10보다 크기 때문에 10의 오른쪽에 저장됨
- 다음 1을 저장하면 숫자 10보다 작고, 5보다 작기때문에 5의 왼쪽에 저장이되고 그다음 6은 10보다 작고 5보다 크기때문에 5의 오른쪽에 저장됨
- 11과 16도 동일한 방식으로 적용되어 최종적으로 그림과 같은 이진 탐색 트리가 생성됨
(5) 이진 탐색 트리 - 검색
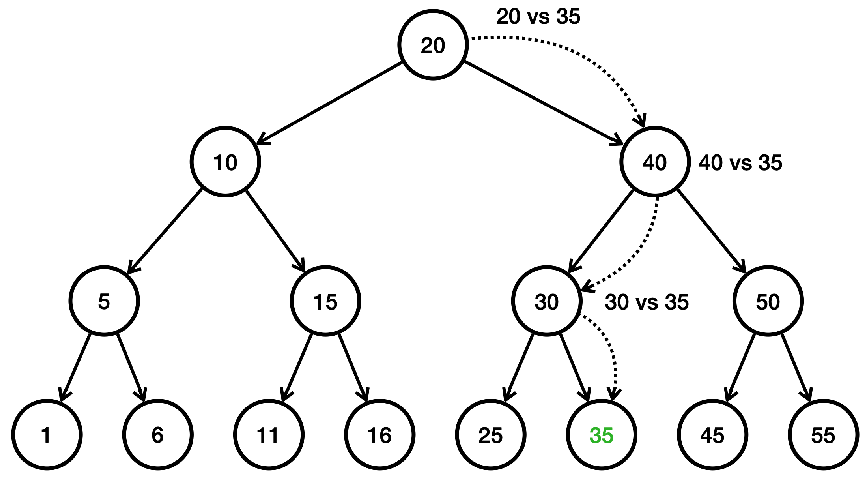
- 그림처럼 15개의 데이터가 들어있다고 가정하고 35를 검색한다고 가정
- 1. 루트인 20과 35를 비교, 35가 더 크기 때문에 오른쪽으로 찾아감
- 2. 40과 35를 비교, 35가 더 작기 때문에 왼쪽으로 찾아감
- 3. 30과 35를 비교, 35가 더 크기 때문에 오른쪽으로 찾아감
- 4. 노드에 있는 값을 비교, 35와 같으므로 35를 찾음
- 데이터가 총 15개인데 4번의 계산으로 필요한 결과를 얻을 수 있었으며 O(n)인 리스트의 검색보다는 빠르고 O(1)인 해시의 검색 보다는 느림
- 이진 탐색 트리 계산의 핵심은 한번에 절반을 날린다는 점임
- 16개가 데이터가 있으면 루트에서 처음 비교를 통해 절반의 데이터를 찾지 않아도 되며 남은 절반의 데이터에서만 찾으면 되고, 여기서도 데이터를 반씩 날리면서 데이터를 찾기 때문에 데이터가 많을수록 검색 효율이 높아짐
(6) 이진 탐색 트리의 빅오 - O(log n)
- 16개 데이터의 경우 단 4번의 비교 만으로 최종 노드에 도달할 수 있음
- 2개의 경우 -> 2로 1번 나누기, log₂(2) = 1
- 4개의 경우 -> 2로 2번 나누기, log₂(4) = 2
- ...
- 32개의 경우 -> 2로 5번 나누기, log₂(32) = 5
- ...
- 1024개의 경우 -> 2로 10번 나누기, log₂(1024) = 10
- 위의 예시 처럼 1024개의 데이터를 단 10번의 계산으로 원하는 결과를 찾을 수 있어 데이터의 크기가 늘어나도 늘어난 만큼 한번의 계산에 절반을 날리는 동작 방식덕분에 O(n)과 비교하여 데이터의 크기가 클 수록 매우 효과적임
- 수학으로 log₂(N) 으로 표기하는데 쉽게 말하면 2로 몇번 나누어서 1에 도달할 수 있는지 계산하는 것임
- 빅오 표기법에서 상수는 사용하지 않으므로 상수를 제외하고 단순히 O(log n)으로 표현함
(7) 이진 탐색 트리와 성능
- 이진 탐색 트리의 검색, 삽입, 삭제의 평균 성능은 O(log n)이지만 트리의 균형이 맞지 않아 최악의 경우에는 O(n)의 성능이 나옴
- 만약 데이터를 1, 5, 6, 10, 15 순서로 입력했다고 가정해보면 트리 구조가 1 -> 5 -> 6 -> 10 -> 15의 구조로 오른쪽으로 치우치게 되면 결과적으로 15를 검색했을 때 데이터의 수인 5만큼 검색을 해야 함
- 이것은 결과적으로 단일 반향 LinkedList와 똑같은 구조가 되어버려서 최악의 경우 O(n)성능이 나옴
(7) 이진 탐색 트리 개선
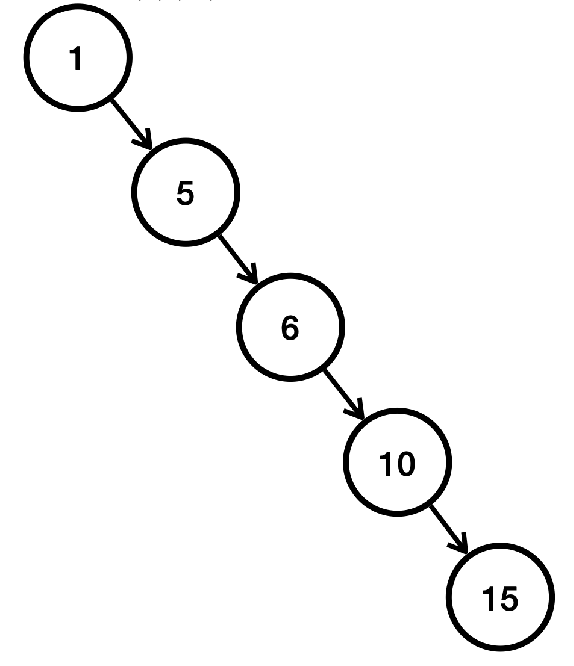
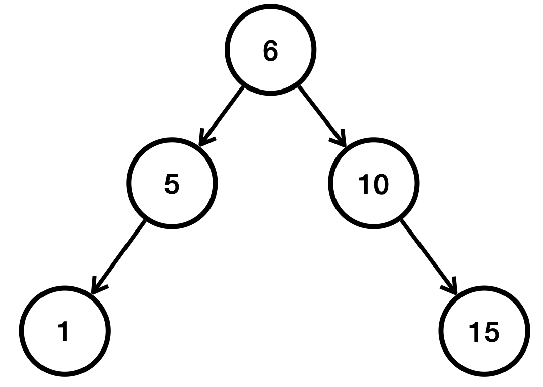
- 이런 문제를 해결하기 위한 다양한 해결 방안이 있는데 일반적인 방법으로 동적으로 균형을 다시 맞추는 것임
- 1, 5, 6, 10, 15 순서로 이진 탐색 트리에 데이터를 입력하면 트리의 균형이 깨지므로 중간에 있는 6을 기준으로 다시 정렬함
- AVL트리, 레드-블랙 트리 같은 균형을 맞추는 다양한 알고리즘이 존재하며 자바의 TreeSet은 레드-블랙 트리를 사용하므로 균형을 지속해서 유지하기 때문에 최악의 경우에도 O(log n)의 성능을 제공함
(8) 이진 탐색 트리 - 순회
- 이진 탐색 트리의 핵심은 입력 순서가 아니라 데이터의 값을 기준으로 정렬해서 보관한다는 점임
- 따라서 정렬된 순서로 데이터를 차례로 조회할 수 있음(순회할 수 있음)
- 데이터를 차례로 순회하려면 중위 순회라는 방법을 사용하면 되는데 왼쪽 서브 트리를 방문한 다음 현재 노드를 처리하고 마지막으로 오른쪽 서브트리를 방문함
- 이 방식은 이진 탐색 트리의 특성상 노드를 오름차순으로 방문함
(9) 중위 순회 순서
- 쉽게 이야기해서 자신의 왼쪽의 모든 노드를 처리하고, 자신의 노드를 처리한다음 자신의 오른쪽 모든 노드를 처리하는 방식임
- 10의 기준에서 왼쪽 서브트리를 방문
- 5의 기준에서 왼쪽 서브트리를 방문
- 1을 출력
- 5자신을 출력
- 5의 기준으로 오른쪽 서브트리를 방문
- 6을 출력
- 10자신을 출력
- 10의 기준에서 오른쪽 서브트리를 방문
- 15의 기준에서 왼쪽 서브트리를 방문
- 11을 출력
- 15의 자신을 출력
- 15의 기준으로 오른쪽 서브트리를 방문
- 16을 출력
- 위의 순서를 보면 1, 5, 6, 10, 11, 15, 16이 정렬된 순서대로 출력된 것을 확인할 수 있음
- 여기서는 TreeSet을 알고 사용하기 위한 정도의 기본적인 트리 이론을 다룬 것이므로 트리 구조에 대해서 더 자세히 알고 싶다면 자료 구조와 알고리즘을 별도로 학습하는 것을 권장함
3) 예제
(1) JavaSetMain
- HashSet, LinkedHashSet, TreeSet 모두 Set 인터페이스를 구현하기 때문에 구현체를 변경하면서 실행할 수 있음
- iterator()를 호출하면 컬렉션을 반복해서 출력할 수 있으며 자세한 내용은 별도로 다룸
- iterator.hasNext(): 다음 데이터가 있는지 확인
- iterator.next(): 다음 데이터를 반환
- 각 자료 구조의 출력
- HashSet: 입력한 순서를 보장하지 않음, O(1)
- LinkedHashSet: 입력한 순서를 정확하게 보장, O(1)이지만 연결 구조를 보관해야하기 때문에 HashSet보다 조금느림
- TreeSet: 데이터 값을 기준으로 정렬함, O(log n)
package collection.set.javaset;
public class JavaSetMain {
public static void main(String[] args) {
run(new HashSet<>());
run(new LinkedHashSet<>());
run(new TreeSet<>());
}
private static void run(Set<String> set) {
System.out.println("set.getClass() = " + set.getClass());
set.add("C");
set.add("B");
set.add("A");
set.add("1");
set.add("2");
Iterator<String> iterator = set.iterator();
while (iterator.hasNext()) {
System.out.print(iterator.next() + " ");
}
System.out.println();
}
}
/* 실행 결과
set.getClass() = class java.util.HashSet
A 1 B 2 C
set.getClass() = class java.util.LinkedHashSet
C B A 1 2
set.getClass() = class java.util.TreeSet
1 2 A B C
*/
** 참고 - TreeSet의 정렬 기준
- TreeSet을 사용할 때 데이터를 정렬하려면 크다, 작다라는 기준이 필요한데, 1, 2, 3, "A", "B", "C"와 같은 기본 데이터는 크다, 작다라는 기준이 명확하기 때문에 정렬이 가능함
- 그러나 우리가 직접 만든 인스턴스들은 크다 작다는 기준을 별도로 제공해야하는데, Comparable, Comparator 인터페이스를 구현해야 하며 이부분은 뒤에서 별도로 다룸
4) 최적화
(1) 자바의 HashSet의 최적화
- 자바의 HashSet은 우리가 직접 구현한 내용과 거의 같지만 추가적인 최적화를 진행함
- 해시 기반 자료 구조를 사용하면 통계적으로 데이터의 수가 배열의 크기를 75% 정도 넘어가면 해시 충돌이 자주 발생하여 성능이 떨어짐
- 데이터가 동적으로 계속 추가되기 때문에 적절한 배열의 크기를 정하는 것은 어렵기 때문에 자바의 HashSet은 데이터의 양이 배열 크기의 75%를 넘어가면 배열의 크기를 2배로 늘리고 2배 늘어난 크기를 기준으로 모든 요소에 해시 인덱스를 다시 적용함
- 자바의 HashSet의 기본 크기는 16이며, 해시 인덱스를 다시 적용하는 시간이 걸리지만 결과적으로 해시 충돌이 줄어들어 기본 성능이 좋아짐
- 이렇게 모든 데이터의 해시 인덱스를 커진 배열에 맞추어 다시 계산하는 과정을 재해싱(rehashing)이라고 함
- ArrayList의 경우 배열의 크기만 늘리면되기 때문에 50%씩 증가하도록 구현했지만 HashSet는 단순히 크기만 늘리는 것이 아니라 재해싱 과정이 있기 때문에 이 과정이 자주 발생하지 않도록 2배씩 크기를 늘림
(2) 정리
- 실무에서는 Set이 필요한 경우 보통 HashSet을 가장 많이 사용함
- 입력 순서 유지, 값 정렬이 필요한 경우에 따라서 LinkedHashSet, TreeSet을 선택하면 됨
2. 문제와 풀이
1) 중복 제거
(1) 문제 설명
- 여러 정수가 입력될 때 중복 값을 제거하고 값을 출력
- 30, 20, 20, 10, 10이 출력되면 중복을 제거하고 출력하면 되며 출력 순서는 관계 없음
더보기
package collection.set.test;
public class UniqueNamesTest1 {
public static void main(String[] args) {
Integer[] inputArr = {30, 20, 20, 10, 10};
// 코드 작성
}
}
실행 결과 - 출력 순서는 관계 없음
20
10
30
(2) 정답
더보기
- HashSet을 사용하면 중복 데이터는 저장되지 않으므로 단순히 HashSet에 값을 입력하고 HashSet을 출력하면 됨
package collection.set.test;
public class UniqueNamesTest1 {
public static void main(String[] args) {
Integer[] inputArr = {30, 20, 20, 10, 10};
Set<Integer> set = new HashSet<>();
for (Integer i : inputArr) {
set.add(i);
}
for (Integer integer : set) {
System.out.println(integer);
}
}
}2) 중복 제거와 입력 순서 유지
(1) 문제 설명
- 문제 1번과 동일한 예제 코드로 중복을 제거하고 출력하되 입력 순서대로 출력
더보기
실행 결과 - 데이터가 입력한 순서대로 출력되어야 함
30
20
10
(2) 정답
더보기
- Set 구현체의 생성자에 배열은 전달할 수 없지만 List는 전달할 수 있으므로 List.of()로 배열을 리스트로 변환 후 Set을 생성하면 간단히 데이터가 입력된 Set 자료구조를 생성할 수 있음
- 자바 1.2부터 제공되는 Arrays.asList()도 있지만 자바9 이상을 사용한다면 List.of()를 권장하며 이에대한 자세한 내용은 뒤에서 설명함
package collection.set.test;
public class UniqueNamesTest2 {
public static void main(String[] args) {
Integer[] inputArr = {30, 20, 20, 10, 10};
Set<Integer> linkedSet = new LinkedHashSet<>(List.of(inputArr));
for (Integer integer : linkedSet) {
System.out.println(integer);
}
}
}3) 중복 제거와 데이터 순서 유지
(1) 문제 설명
- 문제 1번과 동일한 예제 코드로 중복을 제거하고 출력하되 데이터의 값 순서로 출력
더보기
실행 결과 - 데이터의 값 순서대로 출력 되어야 함
10
20
30
(2) 정답
더보기
package collection.set.test;
public class UniqueNamesTest3 {
public static void main(String[] args) {
Integer[] inputArr = {30, 20, 20, 10, 10};
Set<Integer> linkedSet = new TreeSet<>(List.of(inputArr));
for (Integer integer : linkedSet) {
System.out.println(integer);
}
}
}4) 합집합, 교집합, 차집합
(1) 문제 설명
- 집합1: 1, 2, 3, 4, 5
- 집합2: 3, 4, 5, 6, 7
- 제공된 두 숫자 집합의 합집합, 교집합, 차집합 구하고 출력, 출력 순서는 관계 없음
- Set 인터페이스의 주요 메서드를 참고해서 작성
더보기
package collection.set.test;
public class SetOperationsTest {
public static void main(String[] args) {
Set<Integer> set1 = new HashSet<>(List.of(1, 2, 3, 4, 5));
Set<Integer> set2 = new HashSet<>(List.of(3, 4, 5, 6, 7));
//코드 작성
}
}
실행 결과
합집합: [1, 2, 3, 4, 5, 6, 7]
교집합: [3, 4, 5]
차집합: [1, 2]
(2) 정답
더보기
package collection.set.test;
public class SetOperationsTest {
public static void main(String[] args) {
Set<Integer> set1 = new HashSet<>(List.of(1, 2, 3, 4, 5));
Set<Integer> set2 = new HashSet<>(List.of(3, 4, 5, 6, 7));
Set<Integer> union = new HashSet<>(set1);
union.addAll(set2);
System.out.println("합집합: " + union);
Set<Integer> intersection = new HashSet<>(set1);
intersection.retainAll(set2);
System.out.println("교집합: " + intersection);
Set<Integer> difference = new HashSet<>(set1);
difference.removeAll(set2);
System.out.println("차집합: " + difference);
}
}5) Equals, HashCode
(1) 문제 설명
- RectangleTest와 실행 결과를 참고하여 Rectangle 클래스를 완성
- Rectangle 클래스는 width, height가 모두 같으면 같은 값으로 정의함
더보기
package collection.set.test;
public class Rectangle {
private int width;
private int height;
// 코드 작성
}package collection.set.test;
public class RectangleTest {
public static void main(String[] args) {
Set<Rectangle> rectangleSet = new HashSet<>();
rectangleSet.add(new Rectangle(10, 10));
rectangleSet.add(new Rectangle(20, 20));
rectangleSet.add(new Rectangle(20, 20)); //중복
for (Rectangle rectangle : rectangleSet) {
System.out.println("rectangle = " + rectangle);
}
}
}
실행결과
rectangle = Rectangle{width=10, height=10}
rectangle = Rectangle{width=20, height=20}
(2) 정답
더보기
- IDE의 도움을 통해 생성자, equals(), hashCode(), toString()을 오버라이딩하면 끝
package collection.set.test;
import java.util.Objects;
public class Rectangle {
private int width;
private int height;
public Rectangle(int width, int height) {
this.width = width;
this.height = height;
}
@Override
public boolean equals(Object o) {
if (o == null || getClass() != o.getClass()) return false;
Rectangle rectangle = (Rectangle) o;
return width == rectangle.width && height == rectangle.height;
}
@Override
public int hashCode() {
return Objects.hash(width, height);
}
@Override
public String toString() {
return "Rectangle{" +
"width=" + width +
", height=" + height +
'}';
}
}
728x90





